√ Momen Inersia Dan Jawabannya Lengkap

Momen Inersia Dan Jawabannya Lengkap | Pada kesempatan kali ini aku akan memperlihatkan beberapa pola soal momen inersia. Mungkin bagi sebagaian kita soal yang berafiliasi dengan momen inersia sangatlah gampang untuk diselesaikan. Tapi jikalau anda masih merasa kesulitan, maka anda sanggup mencar ilmu melalui soal soal yang telah kami tuliskan di bawah ini. Berikutini adalah  Momen Inersia Dan Jawabannya :

 Momen Inersia Partikel 1

Bola bermassa 100 gram dihubungkan dengan seutas tali yang panjangnya 30 cm menyerupai pada gambar. Momen inersia bola terhadap sumbu AB adalah…

Pembahasan

Diketahui :

Sumbu rotasi yaitu AB

Massa bola (m) = 100 gram = 100/1000 = 0,1 kilogram

Jarak bola dari sumbu rotasi (r) = 30 cm = 0,3 meter

Ditanya : Momen inersia bola (I)

Jawab :

I = m r2 = (0,1 kg)(0,3 m)2

I = (0,1 kg)(0,09 m2)

I = 0,009 kg m2

 Momen Inersia Partikel 2

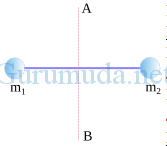
Massa bola m1 yaitu 100 gram dan massa bola m2 yaitu 200 gram. Kedua bola dihubungkan dengan kawat yang memiliki panjang 60 cm dan massanya diabaikan. Sumbu AB terletak di tengah-tengah kawat. Momen inersia sistem kedua bola terhadap sumbu AB adalah…

Pembahasan

Diketahui :

Massa bola 1 (m1) = 100 gram = 100/1000 = 0,1 kilogram

Jarak bola 1 dari sumbu rotasi (r1) = 30 cm = 30/100 = 0,3 meter

Massa bola 2 (m2) = 200 gram = 200/1000 = 0,2 kilogram

Jarak bola 2 dari sumbu rotasi (r2) = 30 cm = 30/100 = 0,3 meter

Ditanya : Momen inersia sistem kedua bola

Jawab :

I = m1 r12 + m2 r22

I = (0,1 kg)(0,3 m)2 + (0,2 kg)(0,3 m)2

I = (0,1 kg)(0,09 m2) + (0,2 kg)(0,09 m2)

I = 0,009 kg m2 + 0,018 kg m2

I = 0,027 kg m2

Soal wacana Momen Inersia EBTANAS 2002

Momen inersia sebuah benda yang berotasi terhadap titik tetap dipengaruhi oleh ….
A. massa benda
B. volume benda
C. massa jenis benda
D. percepatan sudut rotasi
E. kecepatan sudut awal
Pembahasan

Momen inersia yaitu besaran yang menyatakan ukuran kelembaman benda yang mengalami gerak rotasi (seperti massa pada gerak translasi). Momen inersia (I) dirumuskan sebagai:

I = ΣmR2

dengan m yaitu massa benda dan R yaitu jarak benda ke sentra rotasi.
Jadi, momen inersia dipengaruhi oleh massa benda (A).

Soal wacana Momen Inersia UN 2013

Dua bola masing-masing massanya m1 = 2 kg dan m2 = 3 kg dihubungkan dengan batang ringan tak bermassa menyerupai pada gambar.


Jika sistem bola diputar pada sumbu di titik a, besar momen inersia sistem bola yaitu ….
A. 0,24 kg.m2
B. 0,27 kg.m2
C. 0,30 kg.m2
D. 0,31 kg.m2
E. 0,35 kg.m2

Pembahasan: 

m1 = 2 kg
m2 = 3 kg
R1 = 20 cm = 0,2 m
R2 = 30 cm = 0,3 m

Momen inersia pada sistem tersebut adalah:
I = ΣmR2
= m1R12 + m2R22
= 2 × 0,22 + 3 × 0,32
= 0,08 + 0,27
= 0,35

Jadi, besar momen inersia sistem bola tersebut yaitu 0,35 kg.m2 (E).

Soal wacana Momen Inersia UN 2013

Dua bola dihubungkan dengan kawat yang panjangnya 6 m menyerupai pada gambar.



Massa kawat diabaikan dan kedua bola diputar dengan sumbu putar tegak lurus kawat pada benda m1. Besar momen inersia sistem yaitu ….
A. 6 kg.m2
B. 18 kg.m2
C. 36 kg.m2
D. 54 kg.m2
E. 72 kg.m2




Pembahasan

Pada sistem tersebut sumbu putarnya yaitu m1, berarti m1 mati atau tidak diperhitungkan sehingga perumusannya menjadi: 
I = m2R22
= 2 × 62
= 2 × 36
= 72

Jadi, momen inersia sistem tersebut yaitu 72 kg.m2 (E).

Soal wacana Momen Inersia EBTANAS 1998

Perhatikan gambar di bawah ini!

Tiga buah partikel dengan massa m, 2m, dan 3m dipasang pada ujung kerangka yang massanya diabaikan. Sistem terletak pada bidang xy. Jika sistem diputar terhadap sumbu y maka momen inersia sistem yaitu ….
A. 5 ma
B. 7 ma
C. 5 ma2
D. 6 ma2
E. 7 ma2

Pembahasan

Karena sistem diputar terhadap sumbu y maka partikel yang bermassa 2m tidak berfungsi. Berarti hanya partikel yang berada pada sumbu x yang diperhitungkan. Anggap saja partikel di sebelah kiri berindeks (1) dan partikel sebelah kanan berindeks (2). 
m1 = 3m
m2 = m
R1 = a
R2 = 2a

Momen inersia pada sistem tersebut adalah: 
I = ΣmR2
= m1R12 + m2R22
= 3m × a2 + m × (2a)2
= 3ma2 + 4ma2
= 7ma2 

Jadi, momen inersia sistem tersebut yaitu 7 ma2 (E).

Soal wacana Momen Inersia UNAS 2008

Batang AB massanya 2 kg diputar melalui ujung A ternyata momen inersianya 8 kg.m2.

Bila diputar melalui sentra O (AO = OB), momen inersianya menjadi ….

A. 2 kg.m2

B. 4 kg.m2

C. 8 kg.m2

D. 12 kg.m2

E. 16 kg.m2

Pembahasan

Saat batang AB diputar dengan poros A, momen inersianya 8 kg.m2, sehingga panjang batang R sanggup dicari dengan rumus: 

I = mR2

8 = 2R2 

R2 = 4 

R = 2 m

Saat batang AB diputar dengan poros A, massa batang terbagi menjadi dua, demikian juga jarak terhadap poros: 

mA = 1 kg 

mB = 1 kg 

RA = 1 m 

RB = 1 m

Dengan demikian, momen inersianya menjadi: 

I = ΣmR2

= mARA2 + mBRB2

= 1 × 12 + 1 × 12

= 1 + 1

= 2

Jadi, momen inersia pada keadaan tersebut yaitu 2 kg.m2 (A).

Momen Inersia

Empat buah partikel dihubungkan oleh sebuah batang yang massanya diabaikan, ditunjukkan menyerupai gambar di bawah ini. Tentukan momen inersia sistem partikel bila :

• Diputar terhadap poros A 
• Diputar terhadap poros B 

Pembahasan : 

Diputar terhadap poros A

I = ∑m.R2

⇒ I = 2m (0)2 + 4m (r)2 + m (2r)2 + 2m (3r)2 

⇒ I = 0 + 4m r2 + 4m r2 + 18m r2 

⇒ I = 26 m r2 

Diputar terhadap poros B

I = ∑m.R2

⇒ I = 2m (2r)2 + 4m (r)2 + m (0)2 + 2m (r)2 

⇒ I = 8m r2 + 4m r2 + 0 + 2m r2 

⇒ I = 14 m r2 

Momen Inersia

Dengan memakai rumus pergeseran poros, buktikanlah bahwa momen inersia batang homogen yang diputar pada salah satu ujungnya sanggup dihitung dengan rumus I = ⅓ m.l 2.

Pembahasan :

Saat poros bergeser ke salah satu ujung artinya poros digeser sejauh ½l dari pusat, sehingga :

I = 1⁄12 m.l2 + m.(k.l)2
⇒ I = 1⁄12 m.l2 + m.(½.l)2
⇒ I = 1⁄12 m.l2 + ¼ m.l2
⇒ I = (1⁄12 + ¼) m.l2
⇒ I = (1⁄12 + 3⁄12) m.l2
⇒ I = (4⁄12) m.l2
⇒ I = 1⁄3 m.l2
Terbukti.

Momen Inersia

Diketahui sebuah batang homogen bermassa 0,6 kg dan panjang 60 cm. Jika gumpalan lumpur bermassa 20 gram dilempar dan melekat pada salah satu ujung batang, maka tentukanlah momen inersia sistem melalui sentra batang.





Pembahasan :
I = I batang + I lumpur
⇒ I = 1⁄12 m.l2 + mR2
⇒ I = 1⁄12 (0,6).(0,6)2 + 0,02 (0,3)2
⇒ I = 0,018 + 0,0018
⇒ I = 0,0198
⇒ I = 1,98 x 10-2 kg m2

Momen Inersia

Jika sebuah silinder pejal bermassa 2 kg dan berjari-jari 0,1 m diputar melalui sumbu silinder dan segumpal lumpur bermassa 0,2 kg melekat pada jarak 0,05 meter dari pinggir silinder, maka hitunglah momen inersia sistem.

Pembahasan :

I = I silinder + I lumpur
⇒ I = ½ mR2 + m.r2
⇒ I = ½ (2).(0,1)2 + 0,2 (0,05)2
⇒ I = 0,01 + 0,0005
⇒ I = 0,0108
⇒ I = 1,05 x 10-2 kg m2

Demikianlah  Momen Inersia Dan Jawabannya Lengkap. Semoga pola - pola soal tersebut bermanfaat bagi Anda. Anda sanggup juga menggunakannya sebagai materi mencar ilmu di waktu luang anda. Demikianlah  Momen Inersia Dan Jawabannya Lengkap.

Sumber http://kumpulancontohsoall.blogspot.com

√ Momen Gaya Dan Pembahasannya

Momen Gaya Dan Pembahasannya | Pada kesempatan kali ini aku akan memperlihatkan kumpulan contoh soal momen gaya dan pembahasannya. Anda sanggup menggunakannya untuk latihan kemampuan mengerjakan soal soal yang berafiliasi dengan bahan momen gaya. Nah, dibawah ini ialah beberapa contoh soal momen gaya dan pembahasannya. Selamat belajar 

dan Jawaban Momen Gaya Pada Batang dan Bidang I

1. Tiga buah gaya F1 = 15 N, F2 = 5 N dan F3 = 10 N, bekerja pada batang yang panjangnya 50 cm. Jika F1 berjarak 20 cm dari F3, F1 berjarak 30cm dari F2, maka besar resultan momen gaya terhadap poros pada tengah-tengah batang adalah... ( berat batang diabaikan )

Jawaban : 

Poros berada di tengah-tengah batang maka gambarnya menjadi sebagai berikut :

Perhatikan juga lengan momennya harus terhadap poros yang berada di tengah-tengah batang

2 . Pada batang homogen AC yang panjangnya 5 m dikenai gaya F1 dan F2 (seperti pada gambar) . Jika momen gaya yang dialami oleh batang tersebut 120 Nm dan batang berputar berlawanan arah jarum jam pada sumbu putar X. Maka besar F1 adalah….

Jawaban :

Kita menganggap momen gaya berlawanan jarum jam ialah positif.

3 . Gaya-gaya F1 = 8 N, F2 = 10 N, F3 = 12 N bekerja pada bidang persegi yang besisi 10 m. Besar momen gaya total terhadap titik A adalah….

Jawaban :

Gaya F1 dan F2 menghasilkan torsi nol alasannya ialah garis gayanya melalui poros.

dan Jawaban Momen Gaya II

:

Dua roda silinder dengan jari-jari r1 = 30 cm dan r2 = 50 cm disatukan dengan sumbu yang melewati sentra keduanya, menyerupai pada gambar. Hitunglah momen gaya total pada roda gabungan!

Penyelesaian:

Diketahui:

r1 = 30 cm = 0,3 m

r2 = 50 cm = 0,5 m

F1 = -50 N (berlawanan arah jarum jam)

F2 = +50 N (searah jarum jam)

Ditanya: Στ = ... ?

Jawab:

Komponen gaya F2 yang tegak lurus r2 adalah:

F2 sin 60 derajat

sehingga:

Στ = τ2 – τ1 = r2 . F2 sin 60 o – r1 F1 = 0,5 x 50 x (1/2 √3) – (0,3 x 50) = 6,65 Nm2 

dan Pembahasan Torsi III

1. Tentukan momen gaya yang dialami benda pada gambar di bawah ini!

Pembahasan : 

Pada gambar di atas, momen gayanya searah yaitu sama-sama searah jarum jam sehingga resultan momen gayanya merupakan jumlah dari semua torsi yang bekerja. 

∑τ = 6 (6 x 10-2) + 4 (0) + 10 (2 x 10-2) 

⇒ ∑τ = 36 x 10-2 + 20 x 10-2 

⇒ ∑τ = 56 x 10-2 Nm

⇒ ∑τ = 0,56 Nm. 

2. Jika diketahui jarak F1 ke P = 4 m dan Jarak F2 ke P = 2 m, maka tentukan torsi total yang dialami benda pada gambar di bawah ini!

Pembahasan : 

Ingat bahwa untuk mengerjakan soal wacana torsi atau momen gaya, perhatikan gaya harus tegak lurus dengan lengannya. Karena F2 belum tegak lurus dengan lengannya maka harus diproyeksikan terlebih dahulu menjadi F2x dan F2y menyerupai di bawah ini. 

Dari gambar di atas terang terlihat bahwa gaya yang tegak lurus dengan lengannya hanya F2y dan F1 sedangkan F2 dan F2x tidak memenuhi syarat. Dengan begitu, maka momen gaya totalnya ialah :

∑τ = τ2y + τ1

⇒ ∑τ = F2 sin 30o (2) + F1 (4) 

⇒ ∑τ = 20 (½) (2) + 10 (4)

⇒ ∑τ = 20 + 40 

⇒ ∑τ = 60 Nm. 

3. Sebuah batang homogen bermassa 3 kg dan panjang 40 cm, diberi beban 2 kg pada salah satu ujungnya dan ujung lainnya sebagai tumpu. Jika F sebesar 280 N mengarah ke atas bekerja pada jarak 5 cm dari titik tumpu, maka hitunglah momen gayanya.

Pembahasan :

Ingat bahwa batang mempunyai gaya berat yang arahnya ke bawah dan akan berkontribusi dalam perhitungan momen gaya alasannya ialah gaya berat tegak lurus dengan lengannya. Jika digambarkan, gaya-gaya yang bekerja akan menyerupai di bawah ini.

Dari gambar di atas terlihat bahwa torsi akhir gaya berat searah dengan jarum jam sedangkan torsi akhir gaya ke atas berlawan dengan arah jarum jam sehinga momen gaya total ialah : 

∑τ = 20 (0,4) + 30 (0,2) − 280 (0,05)

⇒ ∑τ = 8 + 6 − 14

⇒ ∑τ = 14 − 14

⇒ ∑τ = 0.

Dengan begitu berarti batang tidak berputar atau berada dalam kesetimbangan. 

4. Jika poros perputaran oleh gaya-gaya yang bekerja berada pada titik sentra persegi, maka hitunglah momen gaya total.

Pembahasan :

Pada gambar di atas, gaya yang sudah memenuhi syarat yaitu tegak lurus dengan lengan gayanya ialah F2 dan F3. F1 terang tidak memenuhi syarat dan torsinya sama dengan nol. Sedangkan F4 harus diproyeksikan terlebih dahulu menjadi F4x dan F4y sebaga berikut :

Dari gambar terang terlihat bahwa F4x dan F4y memenuhi syarat yaitu tegak lurus dengan lengannya. Jika R2 ialah lengan F2, R3 ialah lengan F3, R4x ialah lengan F4x dan R4y ialah lengan F4y, maka resultan torsinya ialah : 

∑τ = τ2 + τ3 + τ4x − τ4y

⇒ ∑τ = 20 (0,1) + 10 (0,2) + F4 cos 45o (0,1) − F4 sin 45o (0,2)

⇒ ∑τ = 2 + 2 + 40√2 (½√2) (0,1) − 40√2 (½√2) (0,2)

⇒ ∑τ = 4 + 4 − 8

⇒ ∑τ = 0. 

Soal dan Pembahasan Momen Gaya (Torsi) IV

Kumpulan Soal Momen Gaya (Torsi)

1. Soal dan Pembahasan Momen Gaya/Torsi dalam laman ini menyajikan soal dan pembahasan wacana konsep momen gaya/ torsi yang sering keluar dalam ujian sekolah, ujian nasional dan SBMPTN. Materi momen gaya atau torsi dipelajari oleh siswa kelas XI Sekolah Menengan Atas dan mahasiswa yang mempelajari Fisika Dasar.

Soal Momen Gaya atau Torsi untuk persiapan UH, US, UAN, SBMPTN1. Besaran yang mengakibatkan benda bergerak melingkar adalah...

a. Gaya

b. Torsi

c. Momen Inersia

d. Kecepatan Sudut

d. Momentum Sudut

Kunci Jawaban : B 

Besaran yang mengakibatkan benda bergerak melingkar ialah momen gaya atau torsi.

2. Momen gaya atau torsi ialah besaran fisika pada gerak melingkar yang analogi dengan...

a. Gaya pada gerak lurus

b. Massa pada gerak lurus

c. Kecepatan pada gerak lurus

d. Momen Inersia pada gerak melingkar

e. Momentum Sudur pada gerak melingkar

Kunci Jawaban : A 

Berdasarkan klarifikasi soal no 1, maka kita sanggup analogikan momen gaya atau torsi dengan gaya pada gerak lurus, alasannya ialah yang mengakibatkan benda sanggup bergerak lurus ialah alasannya ialah adanya gaya.

3. Batang AB mempunyai panjang 10 meter dengan poros di titik B diberikan gaya 20 N membentuk sudut siku-siku terhadap batang. Besar torsi yang dialami oleh batang AB adalah...

a. 50 Nm

b. 100 Nm

c. 150 Nm

d. 200 Nm

e. 250 Nm

Kunci Jawaban: D

Besar torsi yang dialami oleh batang dengan gaya membentuk sudut siku-siku di dapatkan dari persamaan torsi τ = F. r. Sin α ( alasannya ialah α = 90o)

τ = F. r

τ = 20 N. 10 m

τ = 200 Nm 

4. Momen gaya yang dialami oleh sistem menyerupai pada gambar di bawah ini ketika poros ada pada titik O adalah...

a. 12 Nm searah jarum jam

b. 28 Nm searah jarum jam

c. 52 Nm searah jarum jam

d. 28 Nm berlawanan arah jarum jam

e. 52 Nm berlawanan arah jarum jam

Kunci Jawaban: B

Untuk soal menyerupai ini, fokus pertama kita ialah menimbulkan titik O sebagai acuan. Jika putaran yang searah jarum jam bernilai positif, maka arah torsi juga kita tulis + dan sebaliknya.

τ = - τ1 + τ2

τ = - F1 r1 Sin 30 + F2 r2 Sin 90

τ = - 12. 2. ½ + 8. 5. 1

τ = - 12 + 40

τ = + 28 Nm

tanda + membuktikan arah putaran akhir torsi di titik O searah jarum jam. 

5. Perhatikan gambar beikut ini!

Batang PQR mempunyai panjang 4 m dan massa 4 kg. Jika F1 = F2 = F3 = 20 N dan panjang PQ 1 m. Besar momen gaya total di titik Q secara adalah...

a. 10 Nm

b. 20 Nm

c. 40 Nm

d. 50 Nm

e. 60 Nm

6. Perhatikan gambar di bawah ini!

Sebuah batang homogen mempunyai panjang 4 m. Tiap ujung batang dikenakan gaya F = 30 N. Maka besar momen kopel gaya pada batang adalah...

a. 60 Nm

b. 80 Nm

c.120 Nm

d.140 Nm

e.160 Nm

Kunci Jawaban: C

Untuk mencari momen kopel kita memakai rumus

M = F. d

Keterangan:

M = Momen kopel

F = Gaya kopel

d = panjang lengan kopel

Maka,

M = 30. 4 = 120 Nm

7. Salah satu contoh penerapan momen gaya dalam kehidupan sehari-hari adalah...

a. Sebuah apel yang diikat dengan tali kemudian diputar.

b. Mengangkat barang memakai pengungkit jenis 1.

c. Mendorong meja pada bidang datar yang licin.

d. Menghentikan benda yang sedang bergerak.

e. Sebuah batang yang terletak pada bidang datar.

Kunci Jawaban: B

Pengungkit jenis 1 ialah pesawat sederhana dimana tuas berada di tengah antara beban dan gaya. Hal ini merupakan penerapan momen gaya dalam kehidupan sehari-hari.

Itulah tadi  Momen Gaya Dan Pembahasannya. semoga dengan adanya soal soal tersebut kita sanggup berguru dan memahami bahan wacana momen gaya. Demikianlah  Momen Gaya Dan Pembahasannya.

Sumber http://kumpulancontohsoall.blogspot.com

√ Kesetimbangan Benda Tegar Dan Pembahasannya

Kesetimbangan Benda Tegar Dan Pembahasannya |  Pada kesempatan kali ini aku akan memperlihatkan beberapa tumpuan soal kesetimbangan benda tegar untuk anda. Na, bagi anda yang sedang  mencari soal untuk materi latihan maka aku telah menuliskannya di bawah ini. Berikut ini adalah  Kesetimbangan Benda Tegar Dan Pembahasannya.

Kesetimbangan Benda Tegar Dan Pembahasannya II

Contoh 1

Pada gambar berikut batang AB beratnya 100 N.

Jika sistem dalam keadaan seimbang, berat beban w ialah ...

Pembahasan:

Diketahui:

Panjang batang AB (lAB) = lAO + lOB = 0,5 + 2 = 2,5 m

Berat batang (wt) = 100 N (berat batang terletak dititik sentra batang yaitu pada titik P sehingga AP = PB = ½ AB = ½ (2,5) = 1,25m)

Perhatikan gambar diatas, terdapat dua gaya yang bekerja pada batang AB yaitu tegangan tali T dan wt dengan poros berada dititik O.

lOB = 2 m

lop = OB – PB = 2 – 1,25 = 0,75 m

Ditanya: berat beban w ?

Jawab:

Sistem dalam keadaan seimbang (∑τ = 0)

Dengan kesepakatan: searah jarum jam (-) dan belawanan arah jarum jam (+), maka:

Karena massa katrol diabaikan, maka w = T. Sehingga w = 37,5 N

Contoh 2

Sebuah batang homogen AB dengan panjang 40 cm dan berat 10 N. Pada ujung batang digantung beban seberat 20 N, batang ditahan oleh tali T sehingga sistem seimbang. Jika sudut yang dibuat oleh tali T 37°, maka hitunglah tegangan tali T!

Pembahasan:

Diketahui:

berat beban (wB) = 20 N

lAB = 40 cm = 0,4 m

berat batang (Wb) = 10 N

lAO = ½ lAB = ½ (0,4) = 0,2 m

α = 37°

Ditanya: tegangan tali T

Jawab:

Contoh 3

Sebuah batang homogen AC dengan panjang panjang 4 m dan massanya 50 kg. Pada ujung C digantungkan beban yang massanya 20 kg. Batang ditahan oleh tali T sehingga sistem seimbang. Jika jarak BC 1 m, maka hitunglah tegangan tali T!

Pembahasan:

Perhatikan gambar berikut, terdapat tiga gaya yang bekerja pada batang AC yaitu tegangan tali T, berat batang, dan berat beban. Dengan poros berada pada titik A.

Diketahui:

massa beban (mB) = 20 kg

berat beban (wB) = mB.g = 20(10) = 200 N

jarak beban terhadap poros: lAC = 4 m

Contoh 3

Sebuah batang homogen AC dengan panjang panjang 4 m dan massanya 50 kg. Pada ujung C digantungkan beban yang massanya 20 kg. Batang ditahan oleh tali T sehingga sistem seimbang. Jika jarak BC 1 m, maka hitunglah tegangan tali T!

Pembahasan:

Perhatikan gambar berikut, terdapat tiga gaya yang bekerja pada batang AC yaitu tegangan tali T, berat batang, dan berat beban. Dengan poros berada pada titik A.

Diketahui:

massa beban (mB) = 20 kg

berat beban (wB) = mB.g = 20(10) = 200 N

jarak beban terhadap poros: lAC = 4 m

massa batang (mb) = 50 kg

Berat batang (wb) = mb.g = 50(10) = 500 N

Titik berat batang berada di titik O, sehingga lAO = ½ lAC = ½ (4) = 2 m

tali T dikaitkan pada titik B, sehingga lAB = lAC – lBC = 4 – 1 = 3 m

α = 30°

Ditanya: tegangan tali T

Jawab:

Contoh 4

Sebuah balok bermassa 5 kg diletakkan diatas papan kayu yang bermassa 10 kg. Papan tersebut bertumpu pada kaki A dan C. Jika jarak beban dari kaki A 1 m dan panjang papan kayu 5 m, maka hitunglah gaya yang dialami oleh kaki A!

Pembahasan:

Berikut ilustrasi gaya-gaya yang bekerja pada papan tersebut.

Perhatikan gambar diatas, terdapat empat buah gaya yang bekerja pada sistem tersebut, yaitu NA, wb, wp, dan Nc. sebab yang ditanyakan gaya normal pada kaki A ( NA ), maka poros berada di titik C. (Catatan: untuk memilih letak titik poros, ambilah gaya yang belum diketahui nilainya, namun tidak ditanyakan dalam soal)

Diketahui:

Panjang papan: lAC = 5 m

massa balok (mb) = 5 kg

berat balok (wb) = mb.g = 5(10) = 50 N

jarak balok terhadap poros (titik C): lBC = lAC – lAB = 5 – 1 = 4 m

massa papan (mp) = 10 kg

Berat papan (wp) = mp.g = 10(10) = 100 N

Titik berat papan berada di titik O, sehingga lOC = ½ lAC = ½ (5) = 2,5 m

Ditanya: Gaya normal pada kaki A ( NA )

Jawab:

Contoh 5

Sebuah tangga seberat 400 N disandarkan pada dinding menyerupai gambar. Jika dinding licin dan lantai kasar, serta tangga sempurna akan tergelincir maka hitunglah koefisien ukiran antara lantai dan tangga!

Pembahasan:

Berikut ilustrasi gaya-gaya yang bekerja pada tangga tersebut. Terdapat empat buah gaya yaitu NB, wt, NA dan f (anak panah berwarna merah).

Diketahui:

Panjang papan: lAB = 10 m

berat tangga (wt) = 400 N

Titik berat tangga berada di titik O, sehingga lOB = lOA = ½ lAB = ½ (10) = 5 m

θ = 53°

Ditanya: Koefisien ukiran antara tangga dan lantai (µ)

Jawab:

Jumlah gaya pada sumbu y (vertikal) dan sumbu x (horizontal) harus nol:

Jumlah torsi di A harus nol (karena yang ditanyakan koefisien ukiran sehingga untuk memudahkan perhitungan, kita pilih titik A sebagai poros). Perhatikan bahwa dalam mengerjakan soal ihwal torsi, gaya yang menyebabkan benda berputar haruslah tegak lurus dengan lengannya. sehingga NB dan wt harus dibuat tegak lurus dengan papan (lihat anak panah berwarna biru)

substitusikan nilai NB pada persamaan (1), sehingga diperoleh:

Jadi koefisien ukiran antara tangga dan lantai sebesar 0,375

Kesetimbangan Benda Tegar II

Soal No.1

Sebuah benda yang massanya 20 kg digantungkan pada ujung tali menyerupai pada gambar. Maka tegangan tali T1 dan T2 berturut-turut ialah ...

Pembahasan : 

Jawaban : E.

Soal No.2

Benda pada gambar dibawah mempunyai berat 100 N digantung dalam keadaan diam. Besar tegangan tali T1 dan T2 ialah berturut-turut ialah ...

A. 80 N dan 60 N

B. 60 N dan 80 N

C. 50 N dan 50 N

D. 30 N dan 40 N

E. 40 N dan 30 N

Pembahasan :

Jawaban : A. 80 N dan 60 N

Soal No.3

Pada gambar dibawah, sistem dalam keadaan setimbang. Perbandingan massa A dengan massa B ialah ...

Pembahasan : 

Jawaban : A

Soal No.4

Perhatikan gambar dibawah!

Massa dan ukiran katrol diabaikan, benda dalam posisi seimbang menyerupai pada gambar di atas. Jika m1 = 10 kg maka massa m2 = ...

Pembahasan : 

Jawaban : C

Soal No.5

Pada sebuah benda bekerja gaya 8 N menyerupai tampak pada gambar. Besar momen gaya terhadap titik P ialah ... Nm

A. 0,96

B. 0,97

C. 0,98

D. 0,99

E. 1

Pembahasan : 

Jawaban : A. 0,96

Soal No.6

Perhatikan gambar dibawah ini!

Pada gambar diatas, Z ialah titik berat batang AB yang massanya 10 kg. Jika sistem dalam keadaan setimbang, maka massa beban C ialah ...

A. 50 kg

B. 30 kg

C. 20 kg

D. 10 kg

E. 4 kg

Pembahasan :

Jawaban : E. 4 kg

Soal No.7

Sistem katrol pada gambar, mempunyai data-data mk = 1 kg, mA = 2 kg , mB = 5 kg, dan katrol K dianggap silinder pejal. Jika ukiran katrol dengan poros dan massa tali diabaikan, serta g = 10 m/s2 maka percepatan benda selama gerak ialah ...

A. 2 m/s2

B. 4 m/s2

C. 6 m/s2

D. 8 m/s2

E. 10 m/s2

Pembahasan : 

Jawaban : B. 4 m/s2

______

Demikianlah  Kesetimbangan Benda Tegar Dan Pembahasannya. Anda sanggup menggunakannya sebagai materi latihan sehingga anda memahami materi ihwal kesetimbangan benda tegar. Sekian  Kesetimbangan Benda Tegar Dan Pembahasannya.

Sumber : aciknadzirah.blogspot.com/search?q=soal-fisika-kesetimbangan-benda-tegar

Sumber http://kumpulancontohsoall.blogspot.com